Computer Graphics

This post contains some knowledges of Computer Graphics. Updating…

在此收录一些关于计算机图形学的问题。更新中…

Common Questions 常见问题

Line Segment Intersection 线段交点

Line Segment $AB$ has $A(x_a, y_a)$ and $B(x_b, y_b)$.

Line Segment $CD​$ has $C(x_c, y_c)​$ and $C(x_c, y_c)​$.

Line Equations:

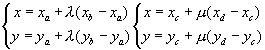
Combine Equations:

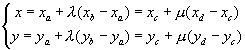
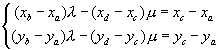
And if the Determinant is 0:

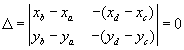
It means line segment overlap or parallel.

If not 0:

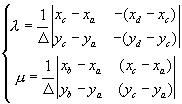
Only when $0\le \lambda \le 1, 0\le \mu \le 1$, two line segments have real intersection, otherwise, the intersection is on their extension.

Point in Triangle 判断点在三角形中

Reference:

GameDev

StackOverflow

Totologic

Method 1

The idea is checking the relative position of point to line plane. If all of them have positive, then it is in the triangle.

bool IsPointInTri(Point p, Point v1, Point v2, Point v3)
{
    if (Sign(p, v1, v2) < 0.0f)
        return false;
    if (Sign(p, v2, v3) < 0.0f)
        return false;
    if (Sign(p, v3, v1) < 0.0f)
        return false;
    // Or > 0.0f in case of opposite winding
    return true;
}

float Sign(Point v1, Point v2, Point v3)
{
  return (v1->x - v3->x) * (v2->y - v3->y) - (v2->x - v3->x) * (v1->y - v3->y);
}

Method 2

Using Barycentric Coordinate System:

$x=a\times x_1 + b \times x_2 + c \times x_3$

$y = a \times y_1 + b \times y_2 + c \times y_3$

$a + b + c = 1$

$$
a = \frac{((y_2 - y_3)\times(x - x_3) + (x_3 - x_2)\times(y - y_3))}{((y_2 - y_3)\times(x_1 - x_3) + (x_3 - x_2)\times(y_1 - y_3))}
$$

$$
b = \frac{((y_3 - y_1)\times(x - x_3) + (x_1 - x_3)\times(y - y_3))}{((y_2 - y_3)\times(x_1 - x_3) + (x_3 - x_2)\times(y_1 - y_3))}
$$

$$
c = 1 - a - b
$$
p lies in T if and only if $0 \le a \le 1$ and $0 \le b \le 1$ and $0 \le c \le 1$.

Basic Knowledge 基础概念

Barycentric Coordinate 重心坐标

Let $x_1, …, x_n$ be the vertices of a simplex in an affine space $A$. If, for some point $p$ in $A$,
$$
(\lambda_1 + \cdots + \lambda_n)p = \lambda_1 x_1 + \cdots +\lambda_n x_n
$$
and at least one of $\lambda_1,…,\lambda_n$ does not vanish then we say the coefficients $\lambda_1,…,\lambda_n$ are barycentric coordinates of $p$ with respect to $x_1, …, x_n$.

Barycentric Coordinate is not unique:

$b\lambda_1,…,b\lambda_n$ where $b \ne 0$.

Detect Collision 测试碰撞

Minkowski difference and Minkowski sum.

Line Sweep Technique 直线扫描转化算法

DDA Algorithm (数值微分法 Digital Differential Analyzer)

中点画线法

Bresenham Algorithm

Circle Sweep Technique 圆的扫描转换算法

Bresenham Algorithm

####Flood Filling & Scan Line Seed Filling

多边形扫描转化算法